3)- Trong đường tròn:
Trong 1 đường tròn thì :
a)- Bình phương đoạn thẳng chắn giữa đường cao bởi đường tròn đường kính là cạnh bên bằng hiệu giữa bình phương cạnh bên với bình phương tổng 2 cạnh đáy.
b)- Hiệu bình phương giữa đường cao và đoạn thẳng chắn giữa trên cạnh ây bởi đường tròn đường kính là cạnh bên bằng 4 lần tích 2 cạnh đáy.
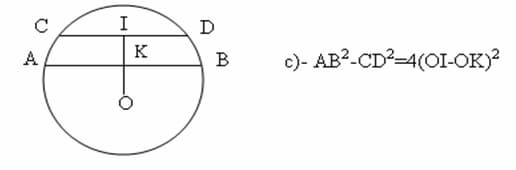
c)- Hiệu bình phương giữa 2 dây cung bằng bốn lần bình phương của hiệu khoảng cách 2 dây cung đến tâm đường tròn.
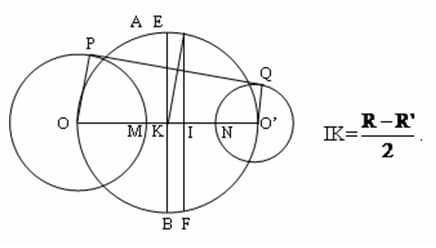
d)- Khoảng cách 2 trung điểm* trên trục nối tâm 2 đường tròn bằng phân nửa hiệu 2 bán kính.
* 2 trung điểm là trung điểm trục nối 2 tâm và trung điểm khoảng cách 2 đường tròn.
4)- Trong tam giác vuông:
Trong một tam giác vuông hiệu giữa hình chiếu 2 cạnh góc vuông xuống cạnh huyền bằng 2 lần hình chiếu trung tuyến từ đỉnh góc vuông xuống cạnh huyền.
Định lý 8:
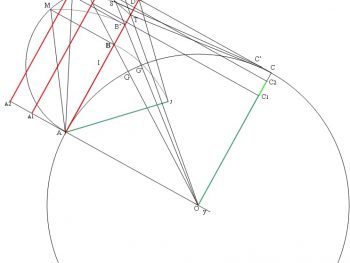
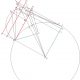
Khi một trong hai đường tròn có chung hai loại tiếp tuyến di chuyển trên trục nối 2 tâm thì Quỹ tích các giao điểm giữa tiếp tuyến chéo nầy và bán kính đường tròn gốc* qua các tiếp điểm của tiếp tuyến chéo kia là nửa đường thẳng giới hạn bởi tiếp tuyến biên (hình 1).
*Đường tròn gốc là đường tròn cố định trong 2 đường tròn có chung 2 loại tiếp tuyến, trong khi đường tròn kia biến đổi, di chuyển trên trục nối 2 tâm.
Định Lý 10:
Khi 1 trong 2 đường tròn có chung 2 loại tiếp tuyến biến đổi, di chuyển trên trục nối 2 tâm thì tiếp tuyến chéo nầy và bán kính đường tròn gốc qua tiếp điểm của tiếp tuyến chéo kia lướt qua những đoạn trung bình nhân bậc 2 luân phiên của nhau trên tiếp tuyến biên (hình 2).
Định Lý 11:
Giao điểm giữa quỹ tích các giao điểm của tiếp tuyến chéo nầy và bán kính đường tròn gốc qua các tiếp điểm của tiếp tuyến chéo kia với tiếp tuyến biên xác định đoạn trung bình nhân bậc 3 giữa các trung bình nhân bậc 2 luân phiên do các tiếp tuyến chéo nầy và bán kính đường tròn gốc qua các tiếp điểm của tiếp tuyến chéo kia định ra trên trên tuyến biên (hình 3).
MỘT SỐ BỔ ĐỀ BỔ TRỢ CHO VIỆC CHỨNG MINH CÁC ĐỊNH LÝ (gọi tắt là Bổ đề)
Để đơn giản việc chứng minh các định lý trong chương trình nầy, đây nêu ra các bổ đề sau:
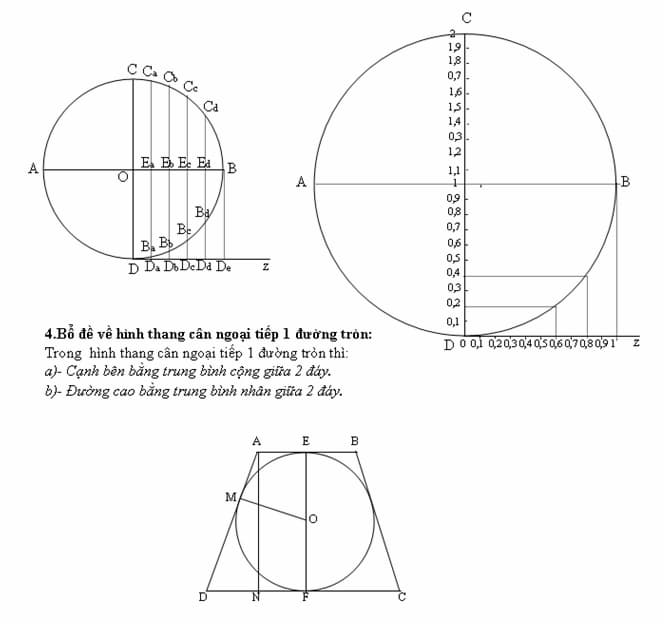
Giải 2 bài toán nan giải của thế giới (Phần 1)